The S = 1/2, I = 1/2 system
For the theoretical description of pulse EPR spectra it is often not necessary to consider the complete spin Hamiltonian. For an S = 1/2 system the quantization axis of the electron spin is mainly determined by the EZI and the influence of the nuclear spins on this axis can be neglected (high-field approximation). Furthermore the coupling between the different nuclear spins, most important in NMR, can be neglected compared to the large coupling of the nuclei to the unpaired electron. It is then possible to divide the complete tensor space into subspaces which contain the interactions between the spin S = 1/2 and a single nuclear spin I. This subspaces can be treated separately and the complete spectrum is obtained by the combination of the results. For spin systems with S > 1/2 a fictitious spin S' = 1/2 can be assigned to the given electron transition if the energy differences between the transitions are larger than the excitation bandwidth of the mw pulses (which is mostly the case) and the same treatment can be applied for the calculation of the spectrum.
The possibility to reduce the dimensionality of the Hamiltonian often allows experimental pulse EPR spectra of I = 1/2 nuclei like 13C and H to be discussed in terms of a simple S = 1/2, I = 1/2 system. This system has the major advantage that it can be treated analytically. The analytical formulae presented in this section are also of importance for the development and understanding of pulse sequences. For the derivation of the formulae, g anisotropy is neglected and the electron spin S is considered to be quantized along the external magnetic field B0. Combination of Eq. (9) and Eq. (12) yields a nuclear spin Hamiltonian for each mS manifold
$$ \mathcal{H}_{\alpha, \beta} = -\frac {g_n{\beta}_n} {h}\mathbf{B}_0 \mathbf{I} + \langle \mathbf{S} \rangle _{\alpha, \beta} \mathbf{A} \mathbf{I} \qquad (14)$$
In this notation <S>α,β is the expectation value of spin of the α/β electron spin states, equal to mS = ±1/2 in our simple case. The nuclear spin Hamiltonian can be expressed in the laboratory frame, where the static magnetic field vector B0 = B0[0 0 1] is taken along the laboratory z-axis. Furthermore it is assumed without loss of generality that the nucleus lies in the xz-plane of the coordinate system. In the resulting expression
$$ \mathcal{H}_{\alpha, \beta} ={\nu}_I {I}_z + m_s \left( AI_z + BI_x \right) = {\nu}_I {I}_z \pm \frac {1}{2} \left(AI_z + BI_x \right)\qquad (15) $$
νI is given by -gnβnB0/h; A = Azz and B = sqrt(Azx2+Azy2), the secular and pseudo-secular parts of the HFI, are functions of hyperfine matrix elements, expressed in the laboratory frame. Diagonalization of this Hamiltonian yields the following expressions for the nuclear frequencies
$$ \left| \begin {matrix} \nu_\alpha \\ \nu_\beta \end {matrix} \right| = \sqrt {\left( \pm \frac {A}{2} + \nu_I \right)^2 + \left(\frac {B}{2} \right)^2}\qquad (16) $$
In first approximation, the coupling between the electron and the nuclear spin is often treated in the point dipole approach, where the electron spin density is considered to be located at a single point in space (e.g. on the central atom of a transition metal nucleus) without delocalization to the ligand nuclei. The hyperfine matrix A is then expressed in its PAS by
$$ \mathbf{A} = \left[ \begin{array}{ccc} {A_1 = A_{\perp}} & {} & {} \\ {} & {A_2 = A_{\perp}} & {} \\ {} & {} & {A_3 = A_{\parallel}} \end{array} \right] = \mathbf{1}a_{iso}+ \left[ \begin{array}{ccc} {-T} & {} & {} \\ {} & {-T} & {} \\ {} & {} & {2T}\end{array} \right] \qquad (17)$$
where the second matrix in Eq. (17), representing the dipolar coupling, is axially symmetric with
$$ {T} = \left ( \frac {\mu_0}{4\pi} \right) \frac {g_eg_n\beta_e\beta_n}{hr^3}\qquad (18)$$
The dipolar coupling constant T is a function of the nuclear gn factor and the electron-nuclear distance r. For isotropic g the largest dipolar coupling (2T) is found along the vector r connecting electron and nucleus. The principal values of these coupling matrices are related to the parameters A and B in Eq. (16) by
$$ {A} = A_{\parallel} \text {cos}^2\theta + A_{\perp} \text {cos}^2\theta = a_\mathrm{iso}+ T \left( 3 \text {cos}\theta^2 -1 \right) \qquad (19)$$
and
$$ {B} = \left( A_{\parallel} - A_{\perp} \right) \text {sin}\theta \text {cos}\theta = 3T\text {sin}\theta \text {cos}\theta\qquad (20)$$
Here θ is the angle between the principal axis of the dipolar coupling matrix (A||) and the magnetic field vector B0. In Fig. 5 these parameters are shown in a schematic drawing. The frequencies να and νβ are centered about νI in the weak coupling limit (νI > |aiso/2+T|). The coupling varies from A|| (θ = 0°, B0 along the z-axis) to A⊥ (θ = 90°, B0 in the equatorial plane).
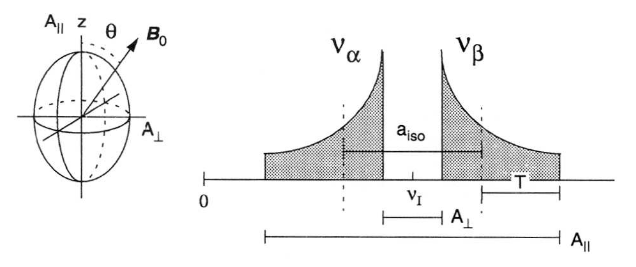
Fig. 5: Schematic drawing of the distribution of the basic frequency features να and νβ for an axial HFI matrix, indicated by the ellipsoid in the inset.
It has already been mentioned before that the two terms in this Hamiltonian describe the magnetic fields, set up at the nucleus by the external magnetic field B0 (first term) and by the electron through the hyperfine coupling (second term). The nuclear spin will be quantized along the resulting of these two contributions. For the interpretation of the spectra it is important to know which contribution is the dominant one. The NZI depends on the gn factor and is in the range of several MHz. The hyperfine coupling (e.g. up to 500 MHz for the copper atom) may thus by far exceed the NZI.
Depending on the dominant interaction one has to consider the weak coupling or strong coupling case which are discussed in the next section. Weak coupling is found e. g. for the water protons in the first coordination sphere of the copper-hexaaquo complex whereas the strong coupling situation is typical for most couplings observable in CW EPR spectra. In the third case, the so called matching range, the two contributions are of equal size. This situation is found for example for the 13C nuclei of the carbonate ions coordinated in a bidentate fashion to the copper nucleus.