Hyperfine Interaction
Two mechanisms with different physical origin can contribute to the coupling between electron and nuclear spins. The first mechanism is the dipole-dipole interaction between the magnetic moments of the electron and nuclear spin in analogy to the classical dipolar interaction between magnetic moments. The energy of this interaction is written as
$$ \mathcal{H}_{dd}=\frac{1}{4 \pi} \frac{\mu_0}{r^3h} {g} \mathcal{\beta_e} {g}_n\mathcal{\beta_n} \left[ \mathbf{SI}-\frac{3}{r^2}(\mathbf{S}\mathbf{r})(\mathbf{I}\mathbf{r}) \right] \qquad (10) $$
where μ0 is the permeability of the vacuum (4π⋅10-7 N·A-2) and r the distance between the two spins (in m), considered to be located at a single point in space (point dipole approximation) and connected by the vector r. The dipole-dipole interaction depends on the relative orientation of the magnetic moments and is thus anisotropic. Purely dipolar interaction is expected e.g. if the electron spin is located in a molecular orbital with a nod at the nucleus (p-, d- or f-orbitals).
The second mechanism becomes important if there is finite spin density of the electron spin at the nucleus. This is the case if there are contributions of s-orbitals to the molecular orbital. The energy term of this so-called Fermi contact interaction is given by
$$ \mathcal{H}_{contact} = \left( \frac{2}{3} \right) \frac{\mu_0}{h} {g} \mathcal{\beta_e} {g}_n\mathcal{\beta_n} \left| \mathcal{\Psi} \left (\begin{array}\text{0}\end{array}\right) \right| ^2 \mathbf{SI} \qquad (11) $$
Here |Ψ(0)|2 is the probability density of the unpaired electron in the s-orbital. The Fermi contact interaction is isotropic and is encountered also in systems with their unpaired electrons in p-, d- or f-orbitals like π-radicals or transition metal ions. The spin density at the nucleus is then induced by mechanisms like configuration interactions or spin polarization.
In general the HFI will be anisotropic due to the dipolar interaction, except for systems where the anisotropic part is averaged out (e.g. by molecular motion in solution). Both mechanisms are then combined to form the hyperfine interaction matrix A and the following term is added to the spin Hamiltonian
$$ \mathcal{H}_{hf} = \mathbf {SAI} \qquad (12) $$
where the hyperfine interaction matrix A is given by
$$ \mathbf{A} = \left[ \begin{array}{ccc} {A}_x & {} & {} \\ {} & {A}_y & {} \\ {} & {} & {A}_2 \end{array} \right] = \mathbf{1}a_{iso} +\left[ \begin{array}{ccc} {A}_x^d & {} & {} \\ {} & {A}_y^d & {} \\ {} & {} & {A}_2 ^d\end{array} \right]\qquad (13)$$
in its PAS. The purely dipolar part is expressed by the second, traceless matrix.
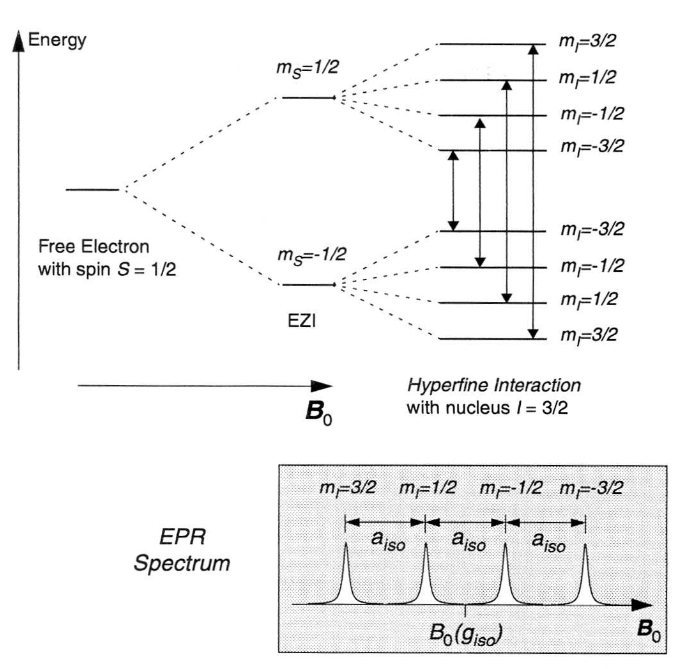
In Fig. 4 the effect of the hyperfine coupling on the energy level diagram and the EPR spectrum is illustrated for the simple case of isotropic EZI and HFI for a spin I = 3/2 (e.g. Cu2+)2. The coupling between the electron and nuclear spin results in a splitting of each electron spin state into 4 levels. MW irradiation causes transitions between levels with ΔmS = ± 1 and ΔmI = 0 (only the electron spin is affected by the microwave irradiation). The four allowed transitions are shown in the energy level diagram. The resulting EPR spectrum consists of four lines centered about giso and split by aiso. The transitions are labelled by their nuclear magnetic spin quantum numbers. For anisotropic hyperfine interactions, powder line shapes are observed for the individual lines as discussed for the g anisotropy.
2 The NZI of the Cu2+ ions is much smaller than the HFI and thus neglected in the drawing. The sign of gn (>0 in Fig. 4) is, however, important for the order of the mI states in the different mS manifolds.