Crystal-Field Splitting and Spin-Orbit Coupling
Although the case discussed so far is a very simple one, there are a number of paramagnetic centers that can be described by a two-level system with resonances around g = 2, e.g. free radicals in solution or transition metal ions such as Ti(III) or 98Mo(V). In most cases, however, more complicated spectra are observed as additional magnetic and electric fields are exerted by the environment of the unpaired electron. In many cases further complications arise from the presence of more than one electron, e.g. for transition metal ions with several unpaired d-electrons (up to five for high-spin Mn2+ or Fe3+) or organic molecules in triplet states. If the interactions between the different magnetic and electric moments and fields are smaller than the electron Zeeman term, they can be described by additional terms in the spin Hamiltonian in Eq. (1) and will lead to further splittings of the energy levels in Fig. 1.
For transition metal ions like VO2+ or Mn2+ the interactions can be much larger than the electron Zeeman term, depending on the nature and the symmetry of the chemical environment of the ion. In this case the energy of the MW frequency may be to small to excite all the transitions. Furthermore only the lowest energy levels are populated with electrons if the energy splitting is much larger than kT, where k is the Boltzmann constant (J·K-1) and T the temperature (K). In this case EPR spectra can only be observed in the ground state manifold of the paramagnetic system.
For transition metal ions in the condensed phase the interactions responsible for the large splittings are the crystal-field (CF) splitting and the spin-orbit coupling (SOC). The combined effect of these two interactions removes the orbital degeneracy of the energy levels for most transition metal ions completely, leaving a non-degenerate ground state, often with zero orbital angular momentum (quenching of the orbital angular momentum).
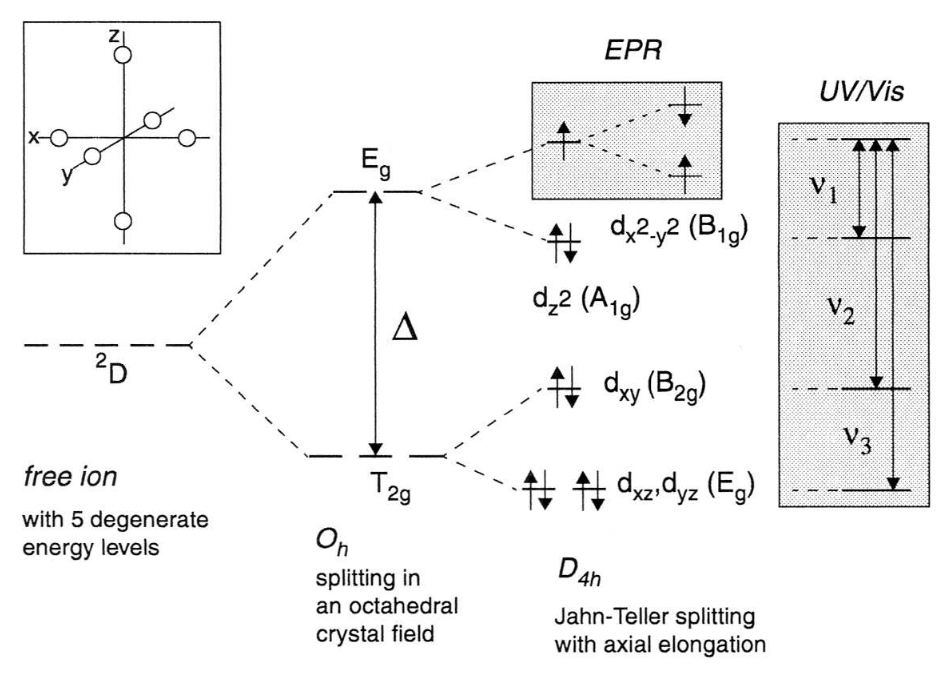
The effect of an octahedral CF on a transition metal ion is illustrated in the first part of Fig. 2 with the arrangement of the ligands drawn schematically in the inset. The energy splitting in the case of octahedral symmetry is given by Δ.
Fig. 2: Illustration of the effect of an octahedral CF on the energy levels of a 3d9 transition metal ion. The resulting energy splitting is Δ. The degeneracy of the orbitals is further lifted by a Jahn-Teller effect through an elongation of the axial bonds, leading to the optical transitions ν1, ν2 and ν3. The geometrical arrangement of the ligands is schematically shown in the inset. The Zeeman splitting of the ground level (B1g) is indicated in the small shaded box.
In the special case of the 3d9 ion in Oh symmetry, the degeneracy of the Eg term is not affected by the SOC, and the Jahn-Teller theorem applies. The orbital degeneracy is lifted and the energy of the system lowered by a displacement of the ligands on the z-axis. An elongation of the coordination octahedron leads to the energy level scheme shown in Fig. 2 with the unpaired electron in the dx2-y2 orbital. The electronic transitions ν1, ν2 and ν3 are indicated by arrows in the large shaded area.
The measurement of EPR spectra is limited to the Zeeman splitting imposed by an external field on the unpaired electron in the non-degenerate dx2-y2 orbital (small shaded area in Fig. 2) and one could think that the spin system can now be described by the spin Hamiltonian in Eq. (1) with S = 1/2 since the ground state is non-degenerate and has only associated spin angular momentum. The ligand field can, however, act on the electron spin through second order effects of the SOC. Since the ground state of most molecules has zero orbital angular momentum due to the quenching by chemical bonding (e.g. radicals) or large CF's (e.g. transition metal ions) the SOC is zero to first order and the influence of the electric CF's on the electron spin negligible. The g-factor should thus have precisely the free-electron value. Interaction between the ground state and excited states, however, admixes small amounts of orbital angular momentum to the ground state which couple to the electron spin and make the electron spin sensitive to its crystalline environment. As a result the g-factor is no longer isotropic - the splitting of the Zeeman levels depends on the symmetry of the ligand field and the orientation of the system in the external magnetic field.
Generally for the description of the EPR spectra in the ground state of a paramagnetic ion, an "effective" spin Hamilton operator is introduced which strongly depends on the involved energy terms and thus on the individual ion and its environment. The influence of the environment is included in a number of parameters such as the g matrix or the zero-field splitting tensor D (for S>1/2). The spin operator S used in the spin Hamiltonian is an "effective" spin, reflecting the number of energy levels involved in the EPR spectrum and does not necessarily refer to the true electron spin quantum number as it is e.g. the case for the Cu2+ ion. However, this has no influence on the theory and no difference will be made between effective spin and true electron spin in the following.