EPR of Cu²⁺ Complexes

$$ \mathcal {H}_\mathrm{sp}= \frac{\beta_e}{h}\mathbf{B}_0 \mathbf{g} \mathbf{S}+\mathbf{S} \mathbf{A}^\mathrm{Cu} \mathbf{I}+\mathcal{H}_N\qquad (26) $$

The electron Zeeman interaction is much larger than the hyperfine coupling to the copper nucleus, expressed by A^Cu. The copper quadrupole interaction is neglected. The g and A^Cu matrices are assumed to be coaxial and axially symmetric and no distinction is made between the two copper isotopes. These simplifying assumptions are often justified in experimental work. The third term H_N describes the ¹³C and proton interactions which are small compared to the first and second term. The CW EPR spectrum is then obtained by neglecting the last term and treating the copper hyperfine interaction e.g. by second order perturbation theory. The EPR spectrum is described by the principal values g_||, g_⊥, A_||, A_⊥ of the g and A^Cu matrices.

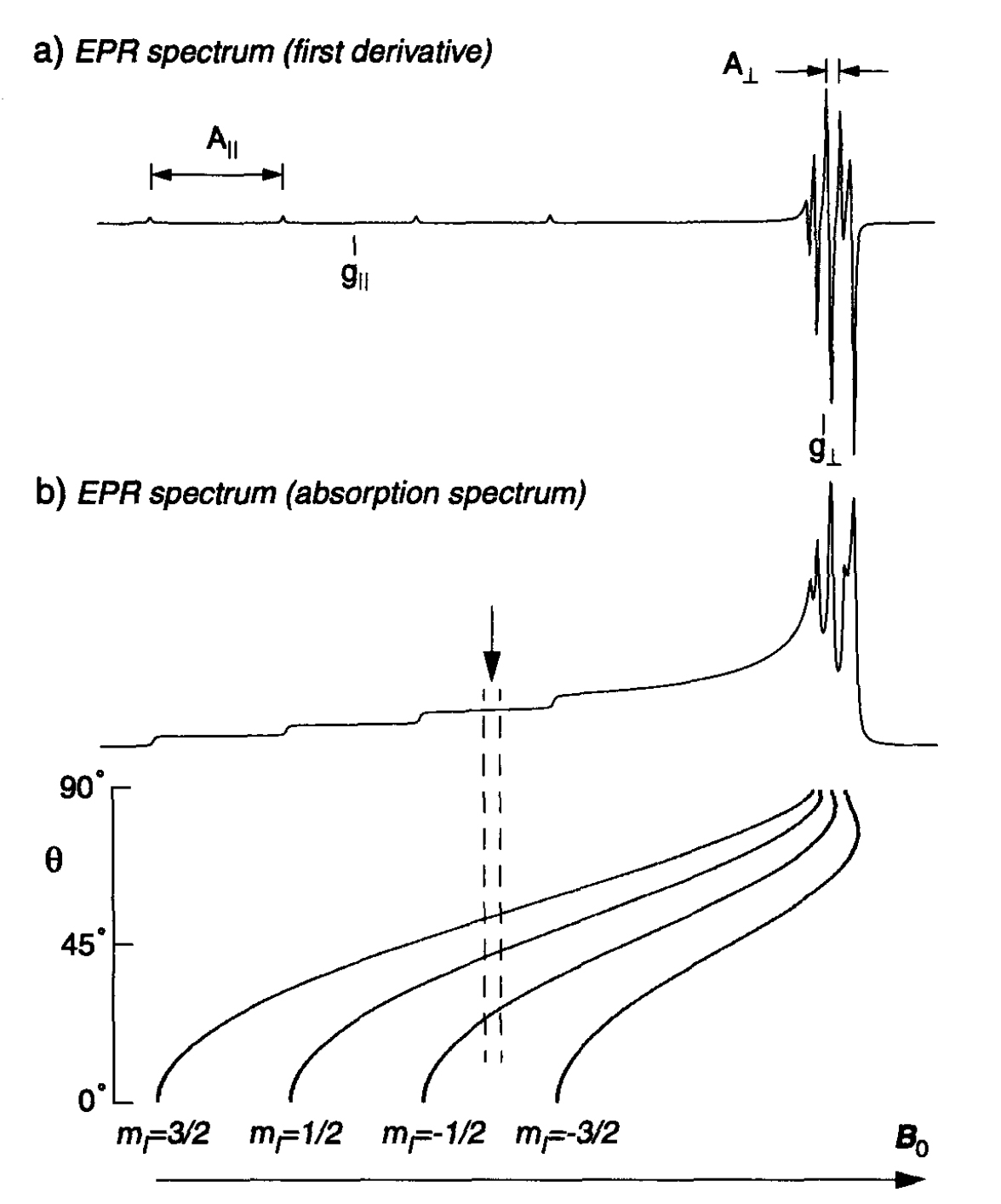
A typical powder EPR spectrum for an axially elongated copper complex is shown in Fig. 10a. The parameters chosen for the simulation of the spectrum are those for a copper-hexaquo complex with g_|| > g_⊥ and A_|| > A_⊥. Due to the amplitude modulation of the B₀ field, CW EPR spectra are usually recorded as first derivatives. In Fig. 10b, the corresponding absorption spectrum is shown. The spectrum is a superposition of four axial powder lines which can be assigned to the different m_I states. The 2D plot shows the contributions of the different m_I states as a function of the angle θ (defined in Fig. 3 as the angle between the z-axis and the external magnetic field vector B₀). In experimental spectra the splitting in the g_⊥ region is often not resolved due to large linewidths whereas the g_|| and A_|| values can usually be determined without difficulties.

The interactions of the electron spin with the weakly coupled I = 1/2 nuclei, described by H_N are usually not resolved in the CW EPR spectra and can only be investigated by applying pulse EPR. Due to the limited bandwidth of the MW pulses only a small part of the EPR spectrum is excited. The dashed lines in Fig. 10b indicate the excitation bandwidth (~50 MHz) for a pulse EPR experiment performed at the B₀ position indicated by the arrow. At a given B₀ position spin packets from different m_I states with different θ values can thus contribute to the spectrum. The pulse EPR spectra of the ¹³C nuclei and protons can be calculated by treating the spin Hamiltonian as for the S = 1/2, I = 1/2 system. More accurate results are obtained by including the g anisotropy in the computation. Diagonalization of the EZI while neglecting the second term in Eq. (26) as the copper hyperfine interaction has no direct influence on the nuclear frequencies leads to the two nuclear Hamiltonians

$$ \mathcal {H}_{\alpha, \beta}= \sum_i \left(\frac {g_n\beta_n}{h}\mathbf{B}_0 \mathbf{I}_i + \langle{\mathbf{S}}\rangle _{\alpha, \beta}\mathbf{A}_{i}^\prime \mathbf{I}_i\right)    \qquad (27) $$